목록Study/확률과 통계 (19)
:: ADVANCE ::
 [확률 및 통계학] Ch 7. 신뢰구간
[확률 및 통계학] Ch 7. 신뢰구간
Ch 7. 신뢰구간 미지의 모수의 값을 추정하기 위해 표본 통계량을 사용하여 통계적 추론을 한다. 표본의 크기가 30이상 이거나 모집단이 정규분포를 따르면서 표준편차 σ를 알 때 모수 μ에 대한 추정을 하기 위해 표본통계량을 사용한다. 통계학에서는 모집단으로부터 표본을 추출하고, 추출된 통계량(표본평균, 표본표준편차)을 통해 모수(모평균, 모표준편차)를 추정하고자 하는 학문이다. 이를 점추정(point estimate)라고 한다. 하지만 점추정만으로는 모수가 얼마나 정밀하게 추정되었는지 알 수 없으므로 존재할 구간을 확률적으로 추정하는 구간추정(interval estimate)이 동시에 사용될 수 있다. 자료의 표본평균을 구하면 되는 듯하다. 즉 점추정값에서 하나의 μ를 구하였지만 모평균이 구하여진 μ값..
 [확률 및 통계학] Ch 6.6 이항분포의 정규근사 2
[확률 및 통계학] Ch 6.6 이항분포의 정규근사 2
Ch 6 6.6 이항분포의 정규근사 [연속성의 보정(correction for continuity)] 이항분포는 이산이고 확률히스토그램으로 나타낼 수 있다. 정확한 이항확률을 계산하기 위하여 x의 각 값에 대해 막대의 폭 1인 값과 히스토그램값의 곱으로 면적을 더하면 된다. 이 때 x의 값은 구간의 중간점에 해당된다. 이항확률을 구하기 위하여 연속적인 정규분포를 사용할 때, x의 모든 값을 포함시키기 위해 0.5 단위만큼 좌우로 움직여야 한다. 예시를 통해 알아보자 문제는 모르지만 np와 nq모두 5를 넘어 정규근사가 가능한 경우이다. 이때 P(X
 [확률 및 통계학] Ch 6.6 이항분포의 정규근사 1
[확률 및 통계학] Ch 6.6 이항분포의 정규근사 1
Ch 6 6.6 이항분포의 정규 근사 .... [확률 및 통계학] 책 129p 에서는 3.4절에서 이항확률을 구했다고 나오나 이건 오타인듯 2.4절에 이항분포가 설명되어 있다. ... 이산이항분포에 대해 복습해보자면 동전을 던지는 시행처럼 Success와 Failure의 2가지 결과만을 갖는 시행인 베르누이(Bernoulli)시행에서 성공할 확률이 p, 실패할 확률을 q (= 1-p)라고 할 때 이며 확률변수 X가 주어질 때 X의 분포를 모수 (n,p)인 이항분포라 한다. 라 표현하였다.
 [확률 및 통계학] Ch 6. 중심극한 정리
[확률 및 통계학] Ch 6. 중심극한 정리
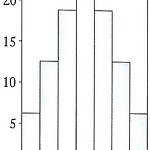
Ch 6 6.5 중심극한 정리 ex) 4개의 요소 { 1 , 3 , 5 , 7 }로 이루어진 모집단에서 복원으로 두 개를 추출. 크기 n = 2의 모든 가능한 표본을 열거하고 각각의 평균을 구하면 표본 평균 표본 평균 1, 1 1 5, 1 3 1, 3 2 5, 3 4 1, 5 3 5, 5 5 1, 7 4 5, 7 6 3, 1 2 7, 1 4 3, 3 3 7, 3 5 3, 5 4 7, 5 6 3, 7 5 7, 7 7 표본평균의 상대도수분포표와 상대도수 히스토그램을 이용하여 표본분포를 그릴 수 있다. 히스토그램의 모양이 종 모양이고 대칭으로 정규곡선과 비슷한 모습을 볼 수 있다. 표본푼포에서 가로축이 표본평균이고 표본평균의 히스토그램이 세로축이 된다. 크기 n의 표본을 뽑아 평균을 구하라는 말은 모집단에서 ..
 [확률 및 통계학] Ch 6. 표준정규분포
[확률 및 통계학] Ch 6. 표준정규분포
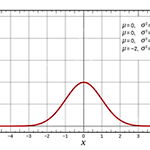
Ch 6. 6.2 표준정규분포 표준정규분포 (Standard normal distribution) - 정규분포 중에서 평균이 0, 표준편차가 1인 정규분포 - 표준정규분포의 수평축은 z-값 (z-score)에 대응된다. - z-값은 어떤 값이 평균으로부터 표준편차의 몇 배 만큼 떨어져 있는지를 나타내는 값이다. 관측치 (X)를 평균이 0, 표준편차가 1이 되도록 z로 치환한다. z-분포라고도 한다. 두 집단이 정규분포를 띈다고 가정하고 그 평균을 통해 크기를 비교하는 것이 z-검정 이다. [표준정규분포의 성질] 1. z가 -3.49에 가까운 경우 누적 면적은 0에 가깝다. 2. z가 증가함에 따라 누적 면적은 증가한다. 3. z = 0 에 대한 누적 면적은 0.5이다. 4. z가 3.49에 가까운 경우 ..
 [확률 및 통계학] Ch 6. 정규분포
[확률 및 통계학] Ch 6. 정규분포
Ch 6. 정규분포 (normal distribution) * 연속형 확률분포 (contiuous probability distribution) - 실수 상에서 구간으로 주어지는 셀 수 없는 연속적인 값을 갖는 확률 변수의 확률분포 정규분포의 사용 예) 측정치들을 모형화하는데 사용하며 인간의 최고혈압, 텔레비젼의 수명이나 주택관리 비용이 정규분포를 따르는 확률변수들이다. 정규분포 (normal distribution) - 종을 엎어 놓은 것과 같은 모양 - 하나의 꼭지점을 가진 완벽한 좌우대칭으로 양꼬리 부분에는 자료가 거의 존재하지 않는다. - 모든 정규분포는 평균과 표준편차에 의해 결정된다. - 즉, 정규분포를 띄는 자료라면, 내용이 어떻던지 간에 평균과 표준편차가 같다면 모두 동일한 정규분포가 된다..
 확률과 통계// 평균과 분산에 대해 정리 // 자료의 탐색
확률과 통계// 평균과 분산에 대해 정리 // 자료의 탐색
확률과 통계.... 왜 공부하는 걸까 모든 자료는 통계분석이 필요하다. 본격적인 통계분석에 들어가기 앞서 어떤 분포를 띄고 있는지, 치우침이나 특이점은 없는지 파악하는 것이 중요하다. 탐색적 자료분석(exploratory data analysis)이란 자료의 특징과 내재하는 구조적 관계를 알아내기 위해 시행하는 모든 방법으로 여기서 얻은 정보를 바탕으로 통계모형을 구축한다. 자료의 분포가 실제로 정규분포에 근사하는지, 그리고 희귀분석을 시행하기 앞서 두 변수가 실제로 선형의 관계를 보이고 있는지 파악하는 것은 매우 중요한 과정이다. 대표값 대표값(representative value)이란 자료를 대표할 수 있는 하나의 값을 의미하며 평균(mean)과 중앙값 등이 있다. 평균(mean)이 가장 널리 사용되..
Ch 5 5.6 사분위수 z는 음수, 0, 양수일 수 있다. z 0 이면, x 값이 평균보다 크다는 뜻이다.
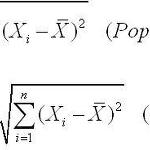 [확률 및 통계학] 표본분산 n과 n-1
[확률 및 통계학] 표본분산 n과 n-1
Population과 Sample은 다르다. Population은 전체 집합이고 Sample은 내가 다룰 수 있는 부분집합의 느낌? 만약 Population을 모두다~ 조사해서 평균과 분산을 구하면 n으로 나누는 것이 맞는 거고 Sample을 추출하여 조사하면 n-1로 나누어야 한다. 또다른 Key point는 지금 SD+에 있는 평균은 Sample의 평균이지 Population의 평균이 아니라는 사실이다. 그렇다면 왜 n-1로 나누는 것일까?? 예를들어 설명해 보자. 알고싶은 사실이 "내 친구 12명중 아스날의 파브레가스의 플레이를 TV를 통해 본 적이 있는 사람의 평균과 표준 편차를 알고 싶다고 하자." 나는 귀찮지만 12명에게 직접 다 물어봐서 Population의 응답 결과를 다 안다고 가정하고 ..
Ch 5. 통계학 5.5 자료의 변동을 재는 방법을 알아보자 가장 쉬운 방법으로 자료의 범위(Range) 가 있다. 자료의 범위를 변동의 척도로 사용하기에는 두 자료만 사용한다는 단점이 있다. 따라서 분산과 표준편차를 사용한다. 표본의 분산이라는 것은 각각의 자료가 평균(표본평균)으로부터 얼마나 떨어져 있는가를 알고자 할 때 나타내는 수치이다. * 각 자료마다의 편차의 합은 0 이므로 편차의 평균을 구하기 위해 편차의 제곱으로 분산을 구한다. 모분산은 N으로 나누는데 표본분산은 n-1을 나누어 준다. 왜 그럴까...?
